ADTs

An Abstract Data Type (ADT) is defined only by its operations (behaviors), not by its implementation.

Note: Swap the removed item with the the last item, and remove the last item. It makes remove() faster.

Among the most important interfaces in the java.util library are those that extend the Collection interface:

  • Lists of things
  • Sets of things
  • Mappings between items
    • Maps also known as associative arrays, associative lists (in Lisp), symbol tables, dictionaries (in Python).

BST

Binary Search Trees

Basics of Tree

A tree consists of:

  • A set of nodes (keys & values).
  • A set of edges that connect nodes.
    • Constraint: There is exactly one path (may contain several edges) between any two nodes. No cycle.

Examples

In a rooted tree, we call one node the root.

  • Every node except the root has exactly one parent.
  • A node with no child is called a leaf.
  • Binary Tree: Every node has either 0, 1, or 2 children (subtrees).

Definition (BST)

The BST is one of the most important ideas that you’ll ever learn in all of computer science.

Can think of the BST as representing a Set (keys) or even a Map (keys and values).

A linked list is great, but it takes a long time to search for an item, even if the list is sorted! If the item is at the end of the list, that would take linear time.

OrderedLinkedList<Character>

Fundamental Problem: Slow search, even though it’s in order.

Recursive Transformation

Definition: A binary search tree is a rooted binary tree with the BST property.

  • Every key in the left subtree is less than X’s key.
  • Every key in the right subtree is greater than X’s key.

Ordering

Ordering must be complete, transitive, and antisymmetric. Given keys $p$ and $q$:

  • Exactly one of $p \prec q$ and $q \prec p$ is true (not both).
  • $p \prec q$ and $q \prec r$ imply $p \prec r$. (transitive)

An example of not complete: Family tree. Compared to your parents, you are “less than”; but compared to your cousins, there is no answer and it’s not a complete thing (in different branches).

One consequence of these rules: No duplicate keys allowed!

It keeps things simple. Most real world implementations follow this rule.

1
2
3
4
5
6
7
8
9
10
11
12
13
private class BST<Key> {
  private Key key;
  private BST left;
  private BST right;

  public BST(Key key, BST left, BST right) {
    this.key = key;
    this.left = left;
    this.right = right;
  }

  public BST(Key key) { this.key = key; }
}
  • For a BST that is bushy (short and fat), we can search in $O(\log N)$ time where $N$ is the number of nodes.
  • For a BST that is spindly (tall and skinny), our search will take $O(N)$ time.

Operations

algs4: BST.java

BST Class

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public class BST<Key extends Comparable<Key>, Value> {
  private Node root;

  private class Node {
    private Key key;
    private Value val;
    private Node left, right;
    private int n;
  }

  public Node(Key key, Value val, int n) {
    this.key = key;
    this.val = val;
    this.n = n;
  }

  /** size */
  public int size() {
    return size(root)
  }

  private int size(Node x) {
    if (x == null) return 0;
    return x.n;
  }

  /** isEmpty */
  public boolean isEmpty() {
    return size(root) == 0;
  }
}

Search/Get

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/** get */
public Value get(Key key) {
  return get(root, key);
}

private Value get(Node x, Key key) {
  if (x == null) return null;
  int cmp = key.compareTo(x.key);
  if (cmp < 0) {
    return get(x.left, key);
  } else if (cmp > 0) {
    return get(x.right, key);
  } else {
    return x.val;
  }
}

Iterative version:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/** get */
public Value getIter(Key key) {
  Node x = root;
  while (x != null) {
    int cmp = key.compareTo(x.key);
    if (cmp < 0) { // left
      x = x.left;
    } else if (cmp > 0) { // right
      x = x.right;
    } else { // found
      return x.val;
    }
  }
  return null; // not found
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* exist - return boolean */
public boolean exist(Key k) {
  Node x = root;
  while (x != null) {
    int cmp = k.compareTo(x.key);
    if (cmp < 0) { // left
      x = x.left;
    } else if (cmp > 0) { // right
      x = x.right;
    } else { // equal
      break;
    }
  }
  return x != null;
}

Insert/Put

Search for key:

  • If found, do nothing
  • If not found:
    • Create new node
    • Set appropriate link

We always insert at a leaf node!

Do not write code like:

1
2
if (T.left == null)       T.left = new BST(key);
else if (T.right == null) T.right = new BST(key);

Recursive version (+ size):

If we need to change the BST, write a helper function that return s a Node object.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public void put(Key key, Value val) {
  root = put(root, key, val);
}

private Node put(Node x, Key key, value val) {
  if (x == null) return new Node(key, val, 1);
  int cmp = key.compareTo(x.key);
  if (cmp < 0) { // left
    x.left = put(x.left, key, val);
  } else if (cmp > 0) { // right
    x.right = put(x.right, key, val);
  } else { // equal
    x.val = val; // just update
  }
  x.n = size(x.left) + size(x.right) + 1; // size can handle null case
  return x;
}

My Code (not good):

Haha! This is the first time I write insert!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public static void insert(BST T, Key sk) {
  Key found = find(T, sk);
  if (found == null) { /* not exist */
    while (true) {
      int result = comp(sk, T.key);
      if (result < 0) { /* left */
        if (T.left == null) {
          T.left = new BST(sk);
          break;
        } else {
          T = T.left;
        }
      } else { /* right (impossible to be equal) */
        if (T.right == null) {
          T.right = new BST(sk);
          break;
        } else {
          T = T.right;
        }
      }
    }
  } /* if exist, do nothing */
}

Iterative version (no size):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public void putIter(Key key, Value val) {
  Node x = root;
  while (x != null) {
    int cmp = key.compareTo(x.key);
    if (cmp < 0) { // left
      if (x.left != null) x = x.left;
      else { x.left = new Node(key, val, 1); return; }
    } else if (cmp > 0) { // right
      if (x.right != null) x = x.right;
      else { x.right = new Node(key, val, 1); return; }
    } else {
      x.val = val; return;
    }
  }
  // optional
  if (x == null) throw new NoSuchElementException();
}

Delete

Consider the following three cases of node $x$:

  • Case 1: No children

    Just sever the parent’s link, and the deleted node will be garbage collected.

    In code, this means return null.

  • Case 2: Has 1 child

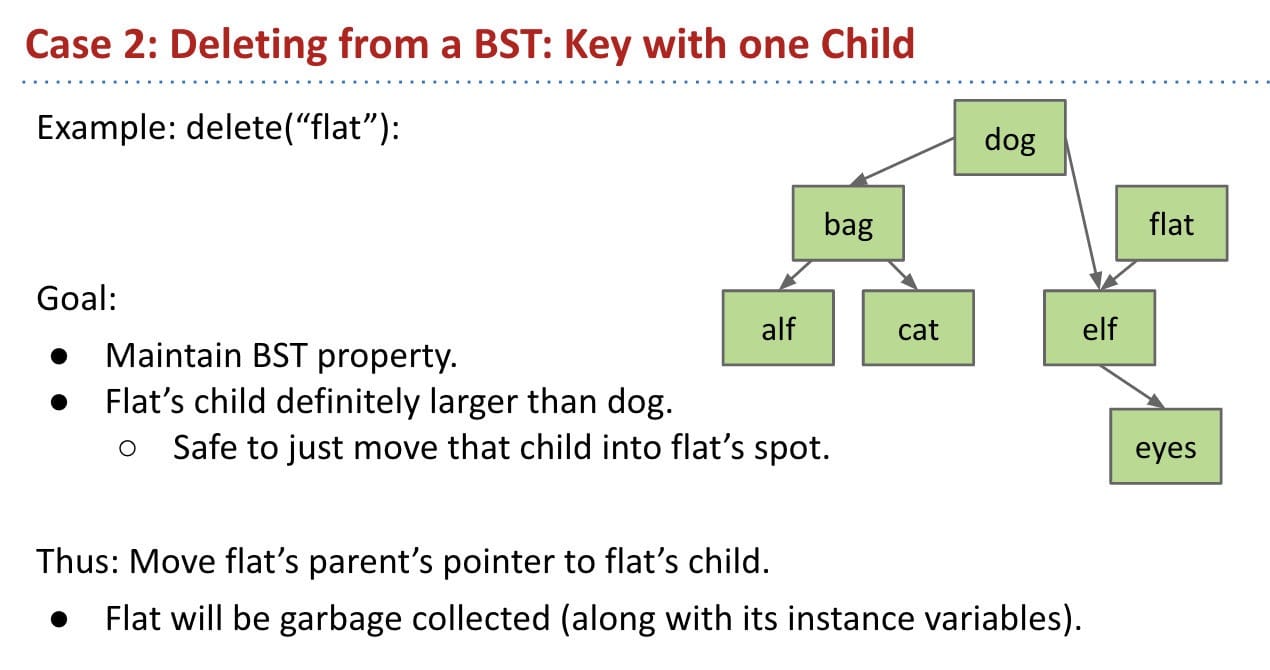
    Case 2: Deleting from a BST: Key with one Child

    We can use recursion to avoid pointer backup.

    What about deleting the root?

  • Case 3: Has 2 children

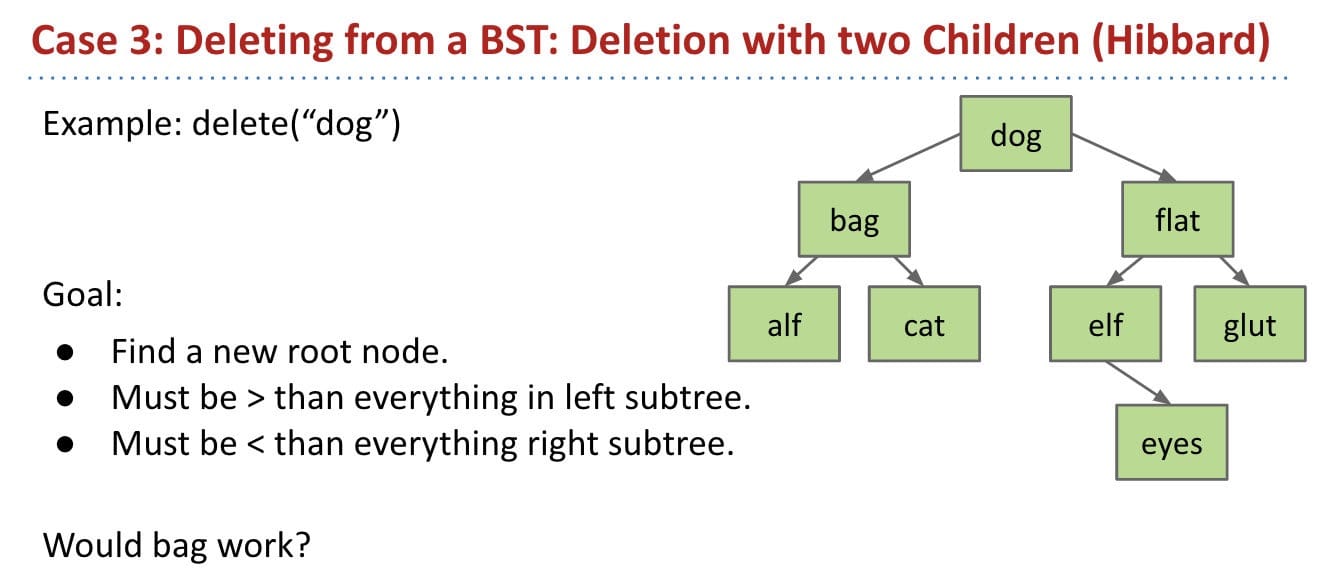
    Case 3: Deleting from a BST: Deleting with two Children (Hibbard)

    No. Moving “bag” is not a good idea.

    We can choose either predecessor "cat" or successor "elf".

    In other words, cat is the largest node in the left tree; elf is the smallest node in the right tree.

    Delete cat or elf, and stick new copy in the root position: This deletion guaranteed to be either case 1 or 2 (no two children). Why?

    • Reason: Predecessor or successor has only one child or no children.

    This method is known as Hibbard deletion.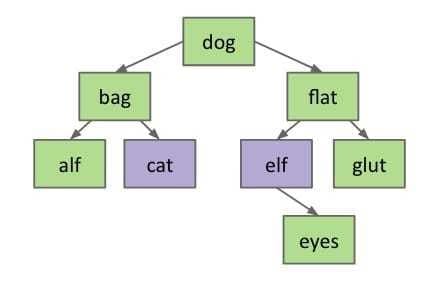

    For example, delete dog and move elf to the root; since we need to delete elf either, eyes will be the left child of flat (case 1).

1
2
3
4
5
6
7
//      dog
//     /   \
//   bag   flat
//   /  \
//  alf  cat
//  /    /
// abc  ?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/** delete */
public Node delete(Node x, Key key) {
  if (x == null) return null; // reach the leaf

  int cmp = key.compareTo(x.key);
  if (cmp < 0) {
    x.left = delete(x.left, key);
  } else if (cmp > 0) {
    x.right = delete(x.right, key);
  } else { // found the key
    if (x.right == null) return x.left;
    if (x.left == null) return x.right;
    Node pre = pred(x); // find the predecessor
    delete(x, pre.key); // delete the predecessor (important! because pre may have a child)
    pre.left = x.left;
    pre.right = x.right;
    x = pre;
    }
  }
  x.n = size(x.left) + size(x.right) + 1;
  return x;
}

private Node pred(Node x) {
  Node p = x.left;
  while (p.right != null) {
    p = p.right;
  }
  return p;
}

Or using min and deleteMin in algs4:

  • [BST.java](https://github.com/junhaowww/algs4/blob/master/ch3-searching/src/BST.java)

DeleteMin

1
2
3
4
5
6
7
8
9
10
11
12
13
public void deleteMin() {
  if (isEmpty()) throw new NoSuchElementException();
  root = deleteMin(root);
}

private Node deleteMin(Node x) {
  if (x.left == null) {
    return x.right;
  }
  x.left = deleteMin(x.left);
  x.n = size(x.left) + size(x.right) + 1;
  return x;
}

Floor

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/** floor */
// return key's previous key
public Key floor(Key key) {
  Node x = floor(root, key);
  if (x == null) throw new NoSuchElementException();
  return x.key;
}

private Node floor(Node x, Key key) {
  if (x == null) return null;
  int cmp = key.compareTo(x.key);
  if (cmp < 0) { // left
    // It gotta be in the left, but I don't care the detail
    return floor(x.left, key);
  } else if (cmp > 0) { // right
    //    4
    //   / \
    //  3   5
    //     / \     // Note: 4 is a potential candidate
    //   4.5  6    // key = 5 / 4.3 / 4.5 / 4.7 / 6 / 5.5 / 8
    //             //       5 / 4   / 4.5 / 4.5 / 6 / 5   / 6
    Node ret = floor(x.right, key);
    if (ret == null) return x;
    else return ret;
  } else { // equal
    return x;
  }
}

Select

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//    4
//   / \
//  3   5   // 5's rank is not 2
//     / \  
//   4.5  6  
public Key select(int k) {  // key 0 ~ size - 1
  if (k < 0 || k >= size()) throw new IllegalArgumentException();
  Node x = select(root, k);
  if (x == null) throw new NoSuchElementException();
  return x.key;
}

// k starts from 0 => conditions look better
private Node select(Node x, int k) {
  if (x == null) return null;
  int t = size(x.left);
  if (k < t) { // left
    return select(x.left, k);
  } else if (k == t) { // middle
    return x;
  } else { // right: k > t
    return select(x.right, k - t - 1); // a new subtree
  }
}

Rank

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//    4
//   / \
//  3   5   // 5's rank is not 2
//     / \  
//   4.5  6  
public int rank(Key key) {
  if (key == null) throw new IllegalArgumentException();
  return rank(root, key);
}

private int rank(Node x, Key key) {
  if (x == null) return -1;
  int cmp = key.compareTo(x.key);
  if (cmp < 0) { // left
    return rank(x.left, key);
  } else if (cmp > 0) { // right
    return size(x.left) + rank(x.right, key);
  } else { // found
    return size(x.left);
  }
}

Range Searching

Note: Consider each subtree as $x$.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Range searching
 */
public Iterable<Key> keys() {
  return keys(min(), max());
}

public Iterable<Key> keys(Key lo, Key hi) {
  Queue<Key> queue = new LinkedList<>();
  keys(root, queue, lo, hi);
  return queue;
}

private void keys(Node x, Queue<Key> queue, Key lo, Key hi) {
  if (x == null) return;
  int cmplo = lo.compareTo(x.key);
  int cmphi = hi.compareTo(x.key);
  if (cmplo < 0) {
    keys(x.left, queue, lo, hi);
  }
  if (cmplo <= 0 && cmphi >= 0) {
    queue.offer(x.key);
  }
  if (cmphi > 0) {
    keys(x.right, queue, lo, hi);
  }
}

Lab 7 (BSTMap)

Lab 7: BSTMap.java & Map61B.java
Algs: BST.java

numberOfNodes(BSTMap b)$\sim \Theta(n)$ (b has $n$ nodes)

z is a positive integer.

What is the running time (in Big O notation) of mystery(b, z)?

1
2
3
4
5
6
7
8
9
10
public Key mystery(BSTMap b, int z) {
  if (z > numberOfNodes(b) || z <= 0)
    return null;
  if (numberOfNodes(b.left) == z-1) // size(b.left) + 1 == z
    return b.root.key;
  else if (numberOfNodes(b.left) > z)
    return mystery(b.left, z);
  else
    return mystery(b.right, z - numberOfNodes(b.left) - 1);
}

Time: $O(\log{N})$ where $N$ is the number of nodes in $b$.

Ex (Discussion & Guide)

C Level

Ex 1 (Orderings)

Give two orderings of the keys A X C S E R H that, when inserted into an empty BST, yield the best case height. Draw the tree.

In order: A C E H R S X

H - C - S - …
H - S - C - …

B Level

Ex 1 (Valid Sequence)

Suppose that a certain BST has keys that are integers between 1 and 10, and we search for 5. Which sequence(s) of keys below are possible during the search for 5?

Each time one level, no backward.

a. 10, 9, 8, 7, 6, 5 (o)
b. 4, 10, 8, 7, 5 (o)
c. 1, 10, 2, 9, 3, 8, 4, 7, 6, 5 (o) a chain
d. 2, 7, 3, 8, 4, 5 (x) 8 > 7
e. 1, 2, 10, 4, 8, 5 (o)

Ex 2 (Commutative)

Is the delete operation commutative? In other words, if we delete $x$, then $y$, do we always get the same tree as if we delete $y$, then $x$?

Maybe yes! Couldn’t think of any case. Me reviewing: Couldn’t find it again.

Ex 3 (#Children)

Problem 1 from the Fall 2014 midterm #2.

  • Either 0 or 2 not-null children (complete tree) - $O(\log N)$
  • Either 0 or 2 children - $O(N)$
  • Either 0 or 1 child - $O(N)$

A+ Level

Ex 1 (Merge)

Problem 3 from the Fall 2009 midterm.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/* The operation is [destructive], and creates no new nodes.
 * In the [worst] case, it takes time [linear] in the total number
 * of items in T and L */
public static IntTree mergeRight(IntTree T, IntTree L) {
  T.left = mergeRight2(T.left, Integer.MAX_VALUE, L);
  /* Why Integer.MAX_VALUE? Consider node 26 (always going right in T;
   * there is no actual succ boundary) */
}

/* Assuming T is a BST, and L is the sentinel of a right-leaning BST,
 * return the result of inserting all items of L that are <= succ in T, 
 * removing them from L. */
private static IntTree mergeRight2(IntTree T, int succ, IntTree L) {
  if (L.left == null) { return T; } /* Done */
  if (T == null) {
    if (L.left.data <= succ) { /* succ is the boundary */
      IntTree p = L.left;
      L.left = L.left.right; /* Delete node */
      /* continue inserting nodes from L, if possible */
      p.right = mergeRight2(null, succ, L); /* Why p.right? Because L is right-leaning */
      return p;  /* connect to T */
      // Why won't do it in one loop (recursive structure for the code below)
    }
  } else { /* T != null */
    /* If go left, succ will be T.data; 
     * if go right, succ will be the previous succ (not changing) */
    if (L.left.data <= T.data) {
      T.left = mergeRight2(T.left, T.data, L);
    } else {
      T.right = mergeRight2(T.right, succ, L); /* for node 11: succ is 12 */
    }
    return T;
  }
}

I think the worst case is $O(L \log{T})$

Ex 2 (Is Valid BST?)

From Discussion 7, Spring 2019.

Buggy version:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class TreeNode {
  int val;
  TreeNode left;
  TreeNode right;
}

public static boolean buggyIsBST(TreeNode T) {
  if (T == null) {
    return true;
  } else if (T.left != null && T.left.val > T.val) {
    return false;
  } else if (T.right != null && T.right.val < T.val) {
    return false;
  } else {
    return buggyIsBST(T.left) && buggyIsBST(T.right);
  }
}

The code just looks at two levels.

Example:

1
2
3
4
5
//       5
//     /   \
//    3     8
//   / \   / \
//  1   6 7   9   (6 is larger than 5)

Bug-free version:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static boolean isBST(TreeNode T) {
  return isBSTHelper(T, Integer.MIN_VALUE , Integer.MAX_VALUE);
}

public static boolean isBSTHelper(TreeNode T, int prev, int next) {
  if (T == null) {
    return true;
  } else if (T.val < prev || T.val > next) {
    return false;
  } else {
    // go left  => update MAX restraint (next)
    // go right => update MIN restraint (prev)
    return isBSTHelper(T.left, prev, T.val) && isBSTHelper(T.right, T.val, next);
  }
}

Challenge Lab 7

Challenge Lab 7: link
Code: link

The Internal Path Length of a BST is defined as the average depth times the number of nodes. Or equivalently, it is the sum of the lengths of the paths to every node. The internal and external path lengths are related by:

$$E = I + 2n$$

where $n$ is the number of internal nodes.

Internal & External Path Length

Implementation of OIPL:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Returns the internal path length for an optimum binary search tree of
 * size N. Examples:
 * N = 1, OIPL: 0
 * N = 2, OIPL: 1
 * N = 3, OIPL: 2
 * N = 4, OIPL: 4
 * N = 5, OIPL: 6
 * N = 6, OIPL: 8
 * N = 7, OIPL: 10
 * N = 8, OIPL: 13
 */
public static int optimalIPL(int N) {
  if (N == 1 || N == 0) {
    return 0;
  }
  int plus = (int) log(2, N);
  return plus + optimalIPL(N - 1);
}

private static double log(int base, int x) {
  return Math.log(x) / Math.log(base);
}

Reference: Research Problem about Average Depth

Randomly picking between successor and predecessor will result in 88% of the starting depth. Nobody knows why this happens.