236. Lowest Common Ancestor of a Binary Tree

Reference: LeetCode EPI 9.3EPI 9.4
Difficulty: Medium

My Post: Summary of Four Java Solutions

Problem

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree. The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).

Note:

• All of the nodes’ values will be unique.
• p and q are different and both values will exist in the binary tree.

Example:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5

Analysis

Methods:

1. Recursion (Brute-Force)

   • Traverse the tree in a depth first manner (postorder). For a tree root, we first go deep into its left and right subtree. Remember you should believe that they will return the LCA node.
     • Since the tree is unique, we don’t need to worry that both left and right calls return an LCA node. So if L or R is not null, just return it immediately.
     • Also, it is a postorder traversal that explore the deepest layer first, so we don’t worry if the returned node is lowest common.
   • If both L and R are null, we should check if the root is the possible LCA by using containsNode() method. It indeed incurs some repeated calculation.

     public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
       if (root == null) {
         return null;
       }
       // left & right (note: each node is unique)
       TreeNode L = lowestCommonAncestor(root.left, p, q);
       if (L != null) return L;
       TreeNode R = lowestCommonAncestor(root.right, p, q);
       if (R != null) return R;
       // root
       if (containsNode(root, p) && containsNode(root, q)) {
         return root;
       }
       return null;
     }
     
     private boolean containsNode(TreeNode root, TreeNode node) {
       if (root == null || node == null) {
         return false;
       }
       return root.val == node.val || containsNode(root.left, node) || containsNode(root.right, node);
     }

     Time: $O(N\log{N})$ or $O(N^2)$
     Space: $O(h)$

2. Recursion (Flag)

   • Traverse the tree in a depth first manner (postorder).
   • If the current node itself is one of p or q, we would mark a variable mid as true and continue the search for the other node in the left and right branches.
   • The LCA node would then be the node for which both the subtree recursions return a true flag, or it can also be the node which itself is one of p or q.
   • If either of the left or the right branch returns true, this means one of the two nodes was found below.
   • If at any point in the traversal, any two of the three flags left, right, or mid become true, this means that we have found the LCA.
   • Note: We don’t return int here because it may accumulate the result making always the root the LCA.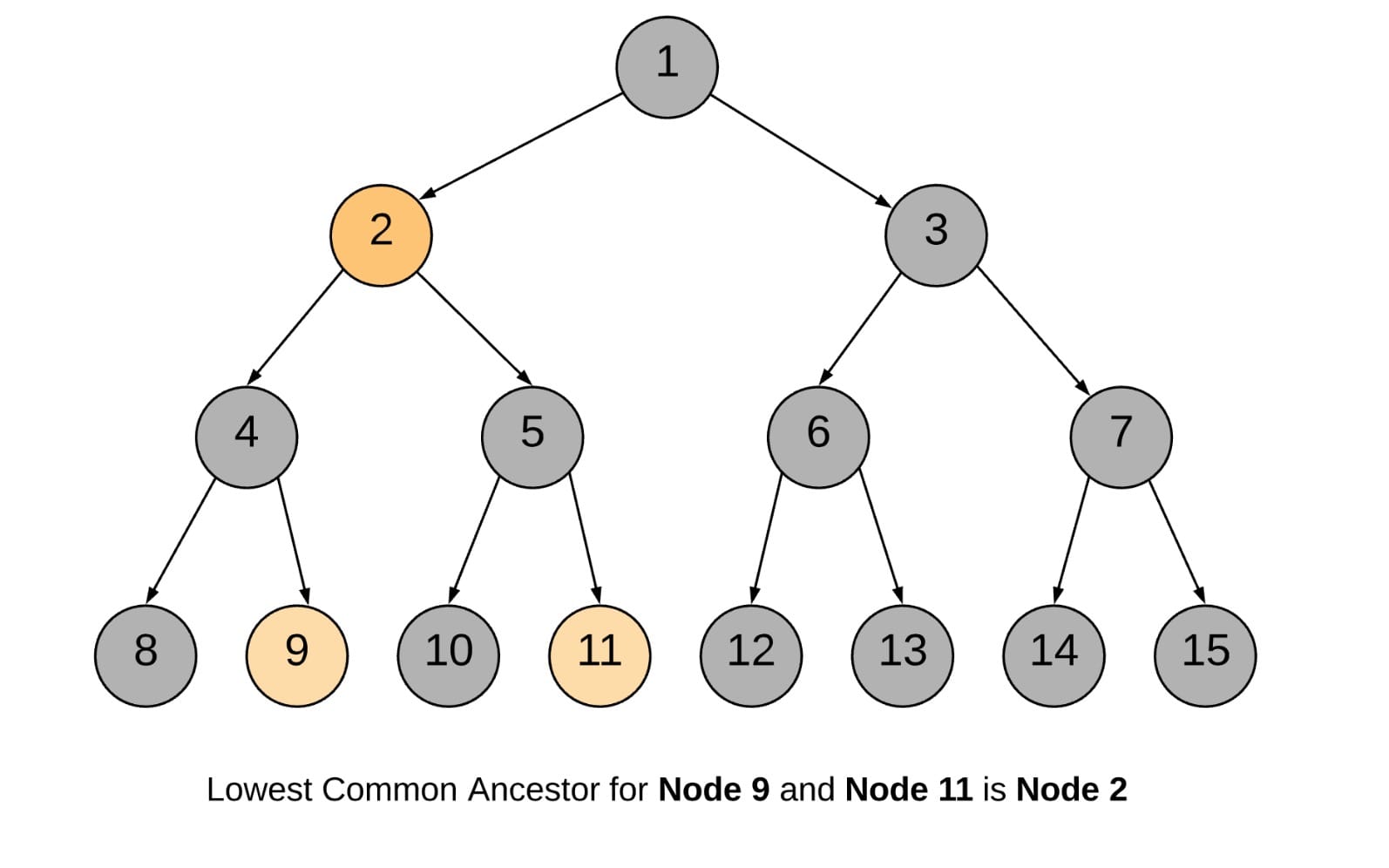
     

     1 --> 2 --> 4 --> 8
     BACKTRACK 8 --> 4
     4 --> 9 (ONE NODE FOUND, return True)
     BACKTRACK 9 --> 4 --> 2
     2 --> 5 --> 10
     BACKTRACK 10 --> 5
     5 --> 11 (ANOTHER NODE FOUND, return True)
     BACKTRACK 11 --> 5 --> 2
     
     2 is the node where we have left = True and right = True and hence it is the lowest common ancestor.

     private TreeNode result;
     
     public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
       if (p == q) return p; // if p and q are the same node
       result = null;
       findNode(root, p, q);
       return result;
     }
     
     private boolean findNode(TreeNode root, TreeNode p, TreeNode q) {
       if (root == null) {
         return false;
       }
       
       int left = findNode(root.left, p, q) ? 1 : 0;
       int right = findNode(root.right, p, q) ? 1 : 0;
       int mid = (root == p || root == q) ? 1 : 0;
       
       if (mid + left + right >= 2) {
         result = root;
       }
       
       return (mid + left + right) > 0;
     }

     Time: $O(N)$
     Space: $O(h)$

3. Iteration (Child-Parent Mapping)

   • Start from the root node and traverse the tree.
   • Until we find p and q both, keep storing the child-parent mappings in a hash map.
   • Once we have found both p and q, we need to store all ancestors of p in a hash set pSet.
   • Then, we traverse through the ancestors of q. If the ancestor is present pSet, this means is the first ancestor common between p and q, which is the LCA node.

     public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
       Map<TreeNode, TreeNode> map = new HashMap<>();
       Set<TreeNode> pSet = new HashSet<>();
       map.put(root, null);
       if (root == null) {
         return null;
       }
       // map all child-parents above p and q
       getParents(root, p, q, map);
       
       // Init pSet
       while (p != null) {
         pSet.add(p);
         p = map.get(p);
       }
       
       // Check if q in pSet
       while (q != null) {
         if (pSet.contains(q)) {
           return q;
         }
         q = map.get(q);
       }
       
       return null;
     }
     
     private void getParents(TreeNode root, TreeNode p, TreeNode q, Map<TreeNode, TreeNode> map) {
       if (root == null) {
         return;
       }
       // Finish - Found them all
       if (map.containsKey(p) && map.containsKey(q)) {
         return;
       }
       
       if (root.left != null) {
         map.put(root.left, root);
       }
       
       if (root.right != null) {
         map.put(root.right, root);
       }
       
       getParents(root.left, p, q, map);
       getParents(root.right, p, q, map);
     }

     Time: $O(N)$
     Space: $O(h)$ consider the set and the map we use, but their sizes are bounded by $h$.

4. Iteration (Parent Pointers, from EPI 9.4)

   • If two nodes are at the same depth, we can move up the tree in tandem from both nodes, stopping at the first node they meet.
   • However, if they are not the same depth, we first ascend the deeper node and make it has the same depth with the other node. Then promote them in tandem.

     public static BinaryTree<Integer> LCA(BinaryTree<Integer> node1,
                                           BinaryTree<Integer> node2) {
       int d1 = getDepth(node1);
       int d2 = getDepth(node2);
       // make node1 > node2, and move node1 first
       if (d1 < d2) {
         int depthTemp = d1;
         BinaryTree<Integer> nodeTemp = node1;
         node1 = node2; node2 = nodeTemp;
         d1 = d2; d2 = depthTemp;
       }
       // ascend d1 to d2
       while (d1 > d2) {
         node1 = node1.parent;
         d1 -= 1;
       }
       // by now d1 == d2
       while (node1 != node2) {
         node1 = node1.parent;
         node2 = node2.parent;
       }
       return node1;
     }
     
     // number of nodes
     private static int getDepth(BinaryTree<Integer> node) {
       int depth = 0;
       while (node != null) {
         node = node.parent;
         depth += 1;
       }
       return depth;
     }

     Time: $O(h)$
     Space: $O(1)$