Reference: LeetCode
Difficulty: Hard

Problem

Two elements of a binary search tree (BST) are swapped by mistake. Recover the tree without changing its structure.

Example: 

1
2
3
4
5
6
7
8
9
10
11
12
Input: [1,3,null,null,2]
   1
  /
 3
  \
   2
Output: [3,1,null,null,2]
   3
  /
 1
  \
   2
1
2
3
4
5
6
7
8
9
10
11
12
Input: [3,1,4,null,null,2]
  3
 / \
1   4
   /
  2
Output: [2,1,4,null,null,3]
  2
 / \
1   4
   /
  3

Follow up:

  • A solution using $O(N)$ space is pretty straightforward. Could you devise a constant space solution?

Analysis

Methods:

  1. Sort An Almost Sorted Array

    • Construct inorder traversal of the tree. It should be an almost sorted list where only two elements are swapped.
    • Identify two swapped elements x and y in an almost sorted array.
      • The algorithm assumes that there is only one inversion which allows cases like:
        • [3 2 1 4] (it can’t be [3 2 1 0] since it needs more than one swapping)
        • [2 1 3 4]
      • So, we update y = nums.get(i + 1) first for two times if necessary, and update x = nums.get(i) only once in the first time.
    • Traverse the tree again and swap x and y.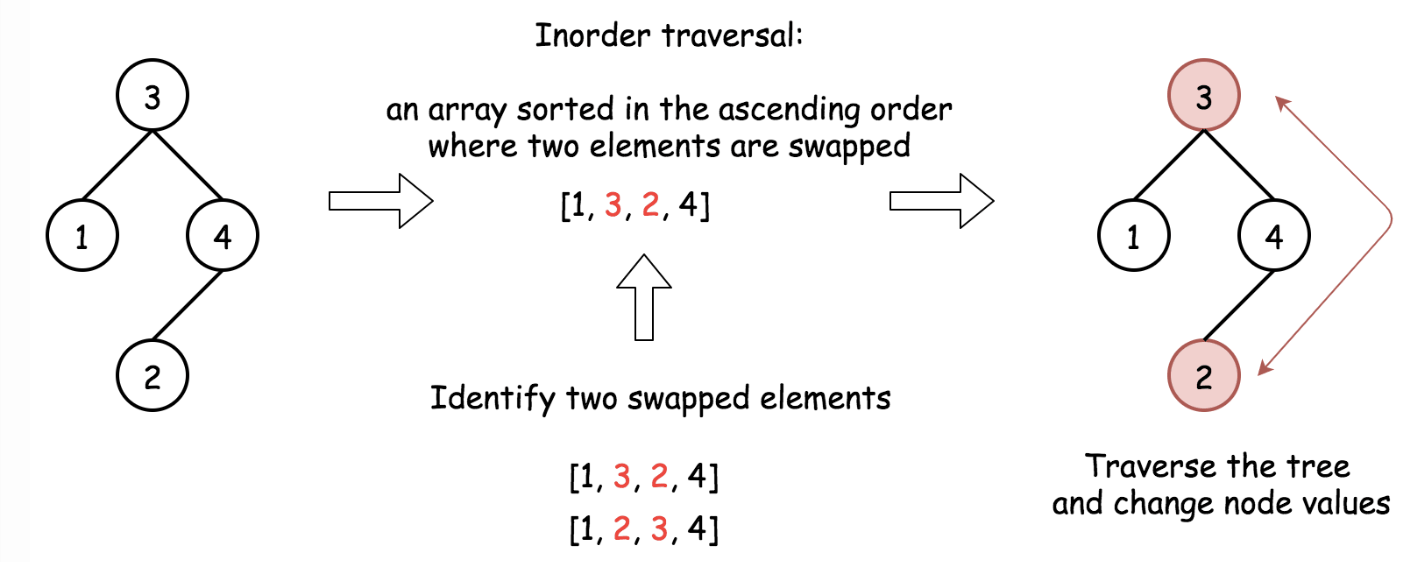
      From LeetCode
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      32
      33
      34
      35
      36
      37
      38
      39
      40
      41
      42
      43
      44
      45
      46
      47
      48
      49
      50
      51
      52
      public void recoverTree(TreeNode root) {
        List<Integer> nums = new ArrayList<>();
        inorder(root, nums);
        int[] swapXY = findTwoSwapped(nums);
        inorderSwap(root, 2, swapXY[0], swapXY[1]);
      }


      // inorder
      private void inorder(TreeNode root, List<Integer> nums) {
        if (root == null) {
          return;
        }
        inorder(root.left, nums);
        nums.add(root.val);
        inorder(root.right, nums);
      }

      // find two swapped
      private int[] findTwoSwapped(List<Integer> nums) {
        int n = nums.size();
        Integer x = null, y = null;
        for (int i = 0; i < n - 1; ++i) {
          // consider: 3  2  1  4
          //           x     y
          // consider: 2  1  3  4
          //           x  y
          if (nums.get(i) > nums.get(i + 1)) { // found
            y = nums.get(i + 1); // update y
            if (x == null) {
              x = nums.get(i); // first (x = 3, y = 2)
            } else {
              break;           // second (x = 3, y = 1)
            }
          }
        }
        return new int[] { x, y };
      }


      // Swap two elements
      private void inorderSwap(TreeNode root, int count, int x, int y) {
        if (root == null || count <= 0) {
          return;
        }
        if (root.val == x || root.val == y) {
          root.val = (root.val == x) ? y : x;
          count -= 1;
        }
        inorderSwap(root.left, count, x, y);
        inorderSwap(root.right, count, x, y);
      }
      Time: $O(N)$ since we apply traversals.
      Space: $O(N)$
      Note: The following approach is based on swapping during inorder traversal. Iterative and recursive approaches here do less than one pass, but they both require up to $O(h)$ space to keep stack. Morris approach needs two passes, but it requires constant space.

  2. One-Pass (Iteration)

    • To identify swapped nodes, track the last node pred in the inorder traversal and compare it with current node. If the current node is smaller than pred, they are swapped nodes. Then we break the traversal after swapping.
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      // One-Pass (Iteration)
      public void recoverTree(TreeNode root) {
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode x = null, y = null, pred = null;
        
        while (root != null || stack.size() > 0) {
          while (root != null) {
            stack.push(root);
            root = root.left;
          }
          root = stack.pop();
          
          if (pred != null && pred.val > root.val) {
            y = root;
            if (x == null) {
              x = pred;
            } else {
              break;
            }
          }
          
          pred = root;
          root = root.right;
        }
        
        // swap
        int temp = x.val;
        x.val = y.val;
        y.val = temp;
      }
      Time: $O(N)$
      Space: $O(h)$

  3. One-Pass (Recursion)

    • Remember to do pred = root!
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      public void recoverTree(TreeNode root) {
        if (root == null) {
          return;
        }
        x = null; y = null; pred = null;
        inorderSwap(root);
        // swap (assume x, y not null)
        int temp = x.val;
        x.val = y.val;
        y.val = temp;
      }

      private void inorderSwap(TreeNode root) {
        if (root == null) {
          return;
        }
        inorderSwap(root.left);

        if (pred != null && pred.val > root.val) {
          y = root;
          if (x == null) {
            x = pred;
          } else {
            return;
          }
        }

        pred = root;

        inorderSwap(root.right);
      }
      Time: $O(N)$
      Space: $O(h)$

  4. Morris Inorder Traversal

    • Marked
    • Time: $O(N)$
    • Space: $O(1)$