Focus: there is a problem; there is a way (it is a problem-solution tutorial).

IntList

IntList - Naked Recursive Structure

Code: IntListEx.java

IntList is a naked recursive data structure.

When you create a public member (i.e. method or variable), be careful, because you’re effectively committing to supporting that member’s behavior exactly as it is now, forever.

Lab 2 (IntList) Code:

sqaureList & catenate & decatenate (iterative + recursive)

IntList.java

存储物理结构/形式：

  • List 列表/线性表（Sequence）
    • Array 数组/顺序存储 (ArrayList or AList)
    • Linked List 链表/链式存储 (LList, SLList, DLList)

逻辑结构（操作）：（可通过上者实现）

  • Queue 队列
  • Stack 栈

SLList

Add Bureaucracy to IntList

Basic Operations: SLList.java

Nested Class

Note: There is a static modifier.

Code: Government.java (code is below)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Government {
  private int treasury = 5;

  /* Thief and Explorer both know Government but not the instance object of Government */

  public static class Thief {
    public void doStuff() {
      Government tmp = null; // ok
      tmp.treasury = 0; // ok - specific object
      treasury = 0; // error - cannot access instance member
    }
  }
  
  public static class Explorer { // ok
    public void doStuff(Government a, Government b) {
      Government favorite = Government.greaterTreasury(a, b);
      System.out.println("The best government has treasury " + favorite.treasury);
    }
  }
}

IntNode: nested class & static class.

static nested class: This saves a bit of memory, because each IntNode no longer needs to keep track of how to access its enclosing SLList (the specific instance, class & other instances are accessible still).

Sentinel

Code: SLList_Sentinel.java

1
2
3
4
5
6
7
8
9
10
11
12
13
/* Original - Without Sentinel */
public void addLast(int x) {
  size += 1;
  if (first == null) {
    first = new IntNode(x, null);
    return;
  }
  IntNode p = first;
  while (p.next != null) { // need to stop at the last one
    p = p.next;
  }
  p.next = new IntNode(x, null);
}

With an SLList, we can now represent an empty list. We simply set first to null and size to 0. However, we have introduced some bugs or variants; namely, because first is now null, any method that tries to access a property of first (like first.item) will return a NullPointerException.

Solution:

  • Renamed first to be sentinel
  • sentinel is never null, its next always points to sentinel node if the list is empty
  • Its item needs to be some integer (whatever)

A list head solves this problem. It is a list node that contains no actual data. A reference or pointer to the list is always a pointer to the head node. The first element of the list is always head.next. Usually the existence of the head is hidden in the class that implements a “linked list with head.” (link)

哨兵顾名思义有巡逻、检查的功能，在我们程序中通过增加哨兵结点往往能够简化边界条件，从而防止对特殊条件的判断，使代码更为简便优雅，在链表中应用最为典型。

单链表中的哨兵结点：首先讨论哨兵结点在单链表中的运用，如果不加哨兵结点在进行头尾删除和插入时需要进行特殊判断。(link)

  • addFirst (no effect)
  • getFirst (no effect)
    1
    2
    3
    4
    public int getFirst() {
      if (sentinel.next == null) return -1;
      return sentinel.next.item; /* sentinel.next could be null */
    }
    Note: Could be addressed by adding the second sentinel or make the first sentinel point to itself.
  • deleteFirst (no effect)
    1
    2
    3
    4
    public deleteFirst() {
      if (sentinel.next == null) return -1;
      // ...
    }
  • addLast (has effect)
    1
    2
    3
    4
    IntNode p = sentinel; /* if p.next is null, while-loop won't be executed */
    while (p.next != null) { p = p.next; } /* p is not null */
    p.next = new IntNode(x, null);
    size += 1;

Invariant

An invariant is a fact about a data structure that is guaranteed to be true (assuming there are no bugs in your code).

A SLList with a sentinel node has at least the following invariants / guarantees:

  • The sentinel reference always points to a sentinel node.
    • which means we can use this node (access its item and next)
  • The first item (if it exists), is always at sentinel.next.item.
  • The size variable is always the total number of items that have been added.
  • Sentinel is null if the list is empty.

Invariants make it easier to reason about code, and also give you specific goals to strive for in making sure your code works.

Slow removeLast

Cache the last pointer! But it’ll make code more complicated.

  • For example: addFirst should update last for the first item in the list, but not in other cases.
    • It’d better to use circular sentinel or two sentinels.
1
2
3
4
5
6
private IntNode last;
public void addLast(int x) {
  last.next = new IntNode(x, null);
  last = last.next;
  size += 1;
}

Compare addLast, getLast, and removeLast, which one is the slowest?

Answer: removeLast. Because last has no access to the previous node’s next.

DLList

What if we add a last pointer (just like the first node)? Not good enough.

Doubly (Go Back)

We only know the last node, but we need information to do:

  • Set last 2nd node’s next to null
  • Set last pointer

Solution: Add .prev

DLList (doubly linked list)

Summary of Improvements (so far)

Sentinel Upgrade

Back pointers allow a list to support adding, getting, and removing the front and back of a list in constant time.

There is a subtle issue with this design where the last pointer sometimes points at the sentinel node (empty list), and sometimes at a real node (special case).

sentinel and last point to the same node

Because the list is not circular! Here are some code for taking care of the last node.

  • addFirst
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    /* L.addFirst(x) */
    public void addFirst(int x) {
      IntNode newNode = new IntNode(x, sentinel.next);
      /* Set the prev of new node */
      newNode.prev = sentinel;
      /* Set the prev of the previous first node - newNode.next may be null */
      if (newNode.next != null) {
        newNode.next.prev = newNode;
      }
      /* Update Last */
      last = sentinel.prev;
      if (size == 0) {
        last = newNode;
      } /* Otherwise, last stays the same */
      size += 1;
    }
  • getFirst
    1
    2
    3
    4
    5
    6
    7
    8
    9
    /* L.getFirst() */
    public int getFirst() {
      /* if size == 0, just return -1 */
      if (size == 0) { /* or sentinel == last */
        return -1;
      }
      /* if size >= 1 */
      return sentinel.next.item;
    }
  • removeFirst
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    /* L.removeFirst() */
    public int removeFirst {
      /* if size == 0, just return -1 */
      if (size == 0) {
        return -1;
      }
      IntNode removedNode = sentinel.next;
      sentinel.next = removedNode.next; /* it's maybe null */
      /* if size == 1, last is still pointing to removedNode */
      if (size == 1) {
        last = sentinel;
      } /* Otherwise if size > 2, last stays the same  */
      size -= 1;
      return removedNode.item;
    }
  • addLast
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    /* L.addLast(x) */
    public void addLast(int x) {
      IntNode newLast = new IntNode(x, null);
      if (size == 0) {
        sentinel.next = newLast;
      } else {
        last.prev.next = newLast; /* not okay if size == 0 */
      }
      newLast.prev = last;
      last = newLast;
      size += 1;
    }
  • getLast
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    /* L.getLast() */
    public int getLast(int x) {
      if (size == 0) {
        return -1;
        /* You may think what if we set sentinel.item to -1, so we don't need the "if" anymore (just return last.item) */
        /* However, it's just okay with getLast. What about other methods? It's not consistent! */
        /* last may point to sentinel and a real node both, while */
        /* sentinel.next always points to the first real node or null */
      }
      return last.item;
    }
  • removeLast
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    /* L.removeLast() */
    public int removeLast() {
      if (size == 0) { /* last.prev == null */
        return -1;
      }
      /* okay with size >= 1 */
      int retItem = last.item; /* the2ndLastNode may be sentinel */
      IntNode the2ndLastNode = last.prev; /* the2ndLastNode  */
      the2ndLastNode.next = null;
      last = the2ndLastNode;
      size -= 1;
      return retItem;
    }

Solution:

Note: There is no last node here, since it breaks invariants.

  • Add a 2nd sentinel node to the back of the list.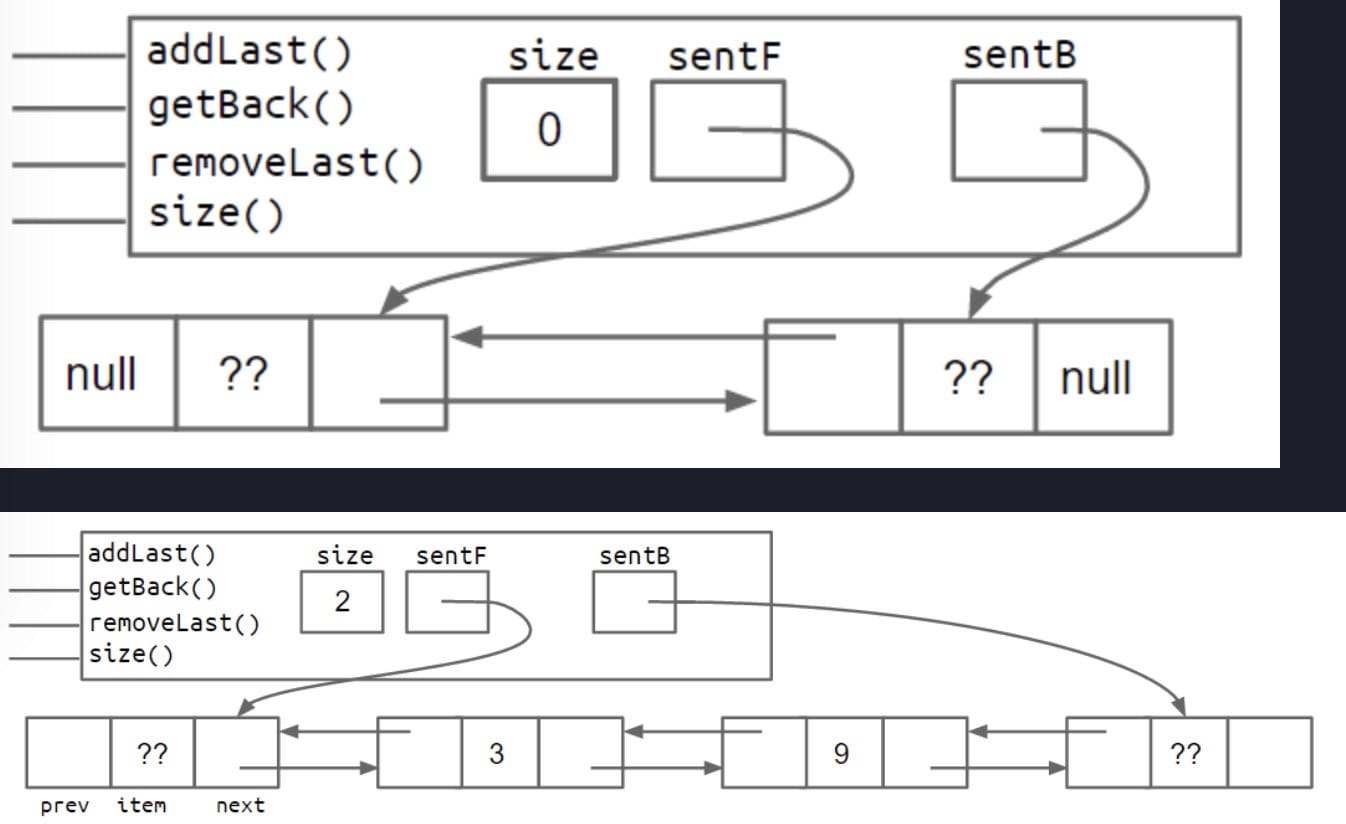

  • Use circular sentinel approach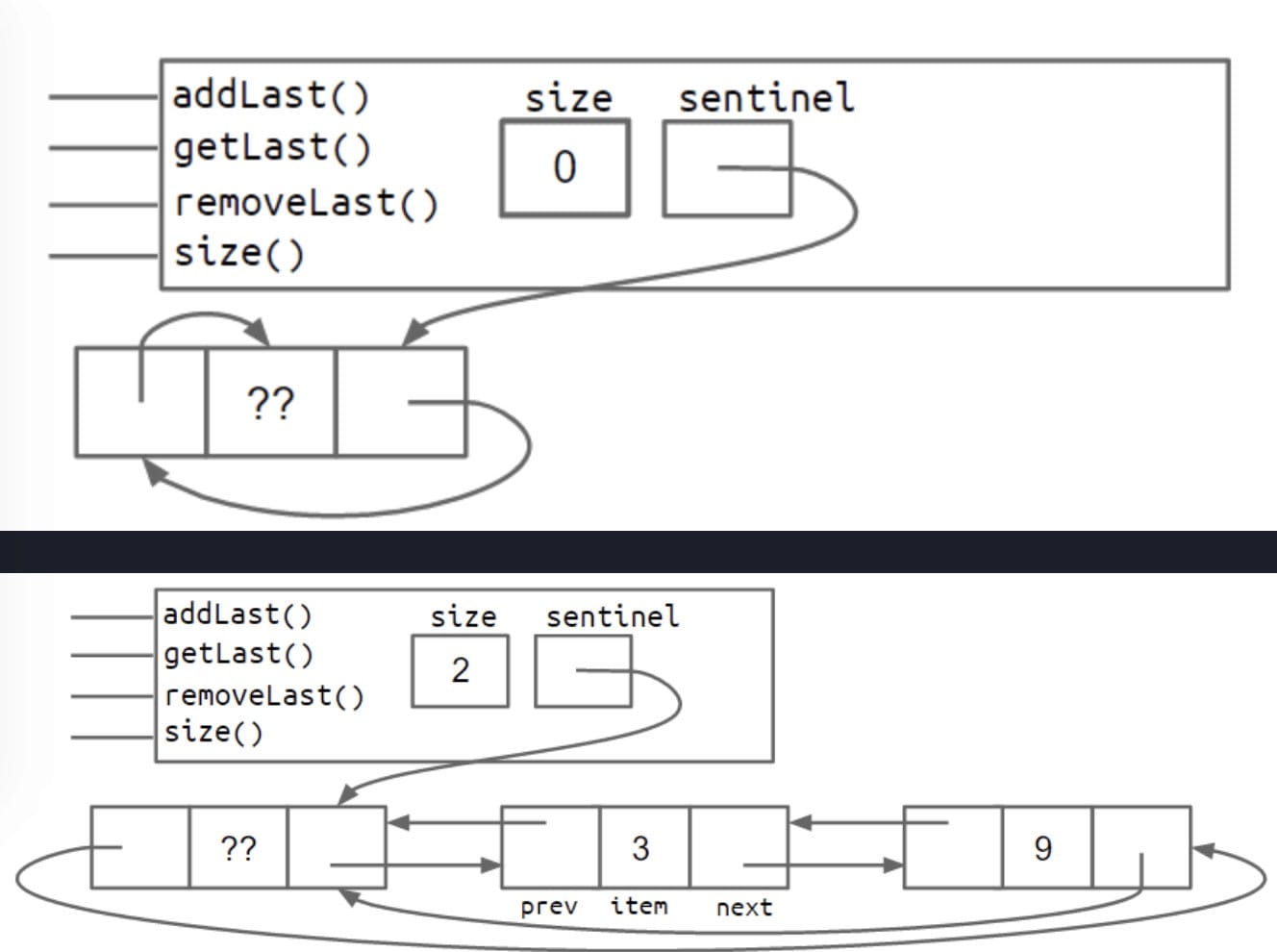


    (Be careful of what the pointers are pointing at!)

Both the two-sentinel and circular sentinel approaches work and result in code that is free of ugly special cases, though I personally find the circular approach to be cleaner and more aesthetically beautiful.

Generic Feature

1
2
3
4
5
6
7
8
9
10
public class DLList<BleepBlorp> {
  private IntNode sentinel;
  private int size;

  public class IntNode {
    public IntNode prev;
    public BleepBlorp item;
    public IntNode next;
    // ...
  }

AList

Array In Java

Java Array: Arrays are a special kind of object which consists of a numbered sequence of memory boxes with fixed integer length.

Unlike other classes, arrays do not have methods.

1
2
// Can omit the new if you are also declaring a variable
int[] w = {9, 10, 11, 12, 13}

1
2
System.arraycopy(b,  0,  x,  3,  2);
//               src si  des di  len

Note: Bound checking only happens in runtime.

2D Array:

Notice the difference:

1
2
3
4
5
6
7
8
9
10
11
12
int[][] pascalsTriangle; /* 1 array */
pascalsTriangle = new int[4][]; /* 4 null values */
int[] rowZero = pascalsTriangle[0];

pascalsTriangle[0] = new int[]{1};
pascalsTriangle[1] = new int[]{1, 1};
pascalsTriangle[2] = new int[]{1, 1, 1};
pascalsTriangle[3] = new int[]{1, 1, 1, 1};
int[][] pascalAgain = new int[][]{{1}, {1, 1}, {1, 1, 1}, {1, 1, 1, 1}}; /* 1 array */

/* 5 arrays */
int[][] matrix = new int[4][4]; /* 4 references to 4 zero arrays */

Performance Puzzle

Performance Puzzle in Linked List:

It turns out that no matter how clever you are, the get method will usually be slower than getBack if we’re using the doubly linked list structure.

This is because, since we only have references to the first and last items of the list, we’ll always need to walk through the list from the front or back to get to the item that we’re trying to retrieve.

In other words, our worst case execution time for get is linear in the size of the entire list. This in contrast to the runtime for getBack, which is constant, no matter the size of the list.

The Way in which you should think:

  • Work out a small example
  • Abstract the pattern
  • Come up with invariants
    • addLast: The next item we want to add, will go into position size.
      • Remember to do size += 1.
    • getLast: The item we want to return is in position size - 1.
    • size: The number of items in the list should be size.

Try to write removeLast. Before starting, decide which of size, items, and items[i] needs to change so that our invariants are preserved after the operation, i.e. so that future calls to our methods provide the user of the list class with the behavior they expect.

  • size should be decreased
  • items should not be changed
  • items[i] should not be changed (no need to “destroy” it)
1
2
3
4
5
6
// AList
public int removeLast() {
  int x = getLast();
  size -= 1;
  return x;
}

Resizing

Issue #1

Raw implementation:

1
2
3
4
5
6
7
8
9
public void addLast(int x) {
  if (size >= items.length) {
    int[] a = new int[size + 100];
    System.arraycopy(items, 0, a, 0, size); /* or items.length */
    items = a;
  }
  items[size] = x;
  size += 1;
}

Better encapsulation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public void addLast(int x) {
  if (size >= items.length) {
    resize(size + 1);
  }
  items[size] = x;
  size += 1;
}

/** Resize the underlying array to the target capacity. */
private void resize(int capacity) {
  int[] a = new int[capacity];
  System.arraycopy(items, 0, a, 0, size); /* or items.length */
  items = a;
}

Geometric Resizing

We can fix our performance problems by growing the size of our array by a multiplicative amount, rather than an additive amount.

Unusably bad (additive amount):

1
2
3
4
5
6
7
public void insertBack(int x) {
  if (size == items.length) {
    resize(size + RFACTOR);
  }
  items[size] = x;
  size += 1;
}

Great performance (multiplicative amount):

1
2
3
4
5
6
7
public void insertBack(int x) {
  if (size == items.length) {
    resize(size * RFACTOR); // = 2 will bring about great improvement
  }
  items[size] = x;
  size += 1;
}

Issue #2

Suppose we have a very rare situation occur which causes us to:

  • Insert 1,000,000,000 items
  • Then remove 990,000,000 items

Our data structure will handle this spike of events as well as it could, but afterwards there is a problem.

An AList should not only be efficient in time, but also efficient in space.

  • Define the usage ratio as R = size / items.length
  • Typical solution: Half array size when R < 0.25

Later we will consider tradeoffs between time and space efficiency for a variety of algorithms and data structures.

Generic Array

In Java, generic array is not supported. We need to do the casting

1
2
3
4
public AList() {
  items = (T[]) new Object[100];
  size = 0;
}

Nulling Out Deleted Items

Unlike integer based ALists, we actually want to null out deleted items. Since Java only destroys unwanted objects when the last reference has been lost. Save memory.

1
2
3
4
5
6
7
8
public T removeLast() { 
  if (size == 0) return null;

  size -= 1;
  T removedItem = items[size];
  items[size] = null; // here
  return removedItem;
}

Obscurantism

We talk of layers of abstraction often in computer science. We also rely on obscurantism. The user of a class does not and should not know how it works.

I like the picture

In Java, we may use private to hide details.

Discussion 3

SLList

The SLList allows us to hide away the inner workings of the linked list and also allows us to store meta-information about the list as a whole such as the size.

Sentinel Nodes

How do we represent an empty linked list? Set first to null?

Goal of sentinel: Make code as simple as generic as possible so we don’t have to have any special cases. (avoid pesky null checks)

DLList

One thing that a list should support is remove(int i) which removes the node whose item is i. With SLList with sentinel, what would we have to do to remove a link?

  • Save a reference to this node
  • Remove its “next” pointer (i)
  • Jump to the node before
  • Reassign next to the node after

We had to traverse the list TWICE in order to do the job. So we add a previous link as well. (don’t quite understand… what if I traverse a node ahead)

AList

Even with the super sophisticated doubly linked list, it’ll take a long time to traverse through the list. So we go back to arrays.

But the bad thing about arrays is that you can’t efficiently add or remove items.

Let’s write a list class that takes advantage of both an array's constant access time and a linked lists adding and removing feature.

AList is a list whose underlying structure is an array.

Ex (D2 + Guide)

Ex 1 (Osmosis - addAdjacent)

Problem: Osmosis

Iterative:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/** addAdjacent(L) */
public void addAdjacent(IntList p) {
  /* if p == null, p.rest will no longer execute */
  if (p.rest == null) {
    /* size <= 1 */
    return;
  }
  /**
   * p.rest != null
   * p ends at the last node finally
   * loop through 1st ~ last 2nd node
   */
  while (p.rest != null) { /* p ends at the last node */
    if (p.first == p.rest.first) {
      /* merge */
      p.first *= 2;
      p.rest = p.rest.rest; /* it's okay if it is null */
      /* Notice: no ++ here */
    } else {
      p = p.rest;
    }
  }
}

Recursive (interesting!):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void addAdjacent(IntList p) {
  if (p == null) return;
  adj(p, p.rest);
}

// helper function - pass previous node recursively
private void adj(IntList prev, IntList current) {
  if (current == null) return;
  if (prev.first == current.first) { /* same as prev */
    prev.first *= 2;
    prev.rest = current.rest; /* maybe null */
  } else {
    adj(current, current.rest);
  }
}

Ex 2 (Square Insertion)

Modify the IntList class so that every time you add a value you “square” the IntList. For example, upon the insertion of 5, the below IntList would transform from:

1 => 2 to 1 => 1 => 2 => 4 => 5

and if 7 was added to the latter IntList, it would become

1 => 1 => 1 => 1 => 2 => 4 => 4 => 16 => 5 => 25 => 7

Additionally, you are provided the constraint that you can only access the size() function one time during the entire process of adding a node.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/** Square Insertion */
public void addLastAndSquare(int x) {
  IntList p = this;
  while (p.rest != null) { /* p won't be null */
    IntList squareNode = new IntList(p.first * p.first, p.rest);
    p.rest = squareNode;
    p = p.rest.rest;
  } /* p stops at the last node */
  /* add node of x */
  IntList newNode = new IntList(x, null);
  /* square the last node  */
  IntList squareNode = new IntList(p.first * p.first, newNode); /* p.rest is null */
  p.rest = squareNode;
  /* if use while (p != null), need an extra pointer to the previous node (to remember) */
  size += 1;
}

But I don’t access the size() function.

1
2
3
4
5
6
7
8
9
10
11
12
13
/** Recursively */
public void addLastAndSquare(int x) {
  helper(this, x);
}
private IntList helper(IntList L, int x) {
  if (L == null) { // the last node
    return new IntList(x, null);
  }
  IntList squared = new IntList(x * x, L.rest);
  L.rest = squared;
  squared.rest = helper(square.rest, x);
  return L
}

Ex 3 (Arrrrghrays)

Problem: link
Code: Arrrrghrays.java

第一列不会发生重复，因为加入的时候已经杜绝这种情况了。

Note: for every p[i], j will start over!

The 1st half of the problem took me half a day to think about… ‘cause I thought I was required to implement sorting in this function :(

画个图才好理解

The 2nd half of the problem took me another half a day to think about… ‘cause I was not sure about:

  • groupByLat, sortByLat, sortHalfLong should be in what kind of orders?
    • Since the parameter of sortByLat is Piece[][], it should follow groupByLat.
  • The most confusing one is sortHalfLong, because there could be 2 situations (the length is even or odd). I spent a lot of time on the implementation of the function, but I kind of misinterpreted its purpose.
  • In the solution, each row has the same latitude, so we need to halfsoft it by longitude… okay… I see… It provides halfsoft on purpose… so we have a chance to practice System.arraycopy
  • System.arraycopy(src, srcPos, dest, destPos, length)
    • upper, lower, mid (learn this pattern)
      • length = 3 (odd)
        • upper = (3.0 / 2 = 1.5) = 2
        • lower = (3.0 / 2 = 1.5) = 1
        • (0 ~ lower is the 1st half, upper could be the length of it)
      • length = 4 (even)
        • upper = (4.0 / 2 = 2.0) = 2
        • lower = (4.0 / 2 = 2.0) = 2
        • For even numbers, upper and lower are the same
    • System.arraycopy(halfsort, 0, tmp, lower, upper);
    • System.arraycopy(halfsort, upper, tmp, 0, lower);
  • You know what. I am confused again, so I’d better test it out.
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    public static void main(String[] args) {
      int[] a = {1, 2, 3};
      int[] b = {0, 0, 0};
      int upper = (int) Math.ceil((double) a.length / 2);
      int lower = (int) Math.floor((double) b.length / 2);
      System.arraycopy(a, 0, b, lower, upper);
      System.arraycopy(a, upper, b, 0, lower);

      System.out.println("a: " + Arrays.toString(a));
      System.out.println("b: " + Arrays.toString(b));
    }
    The output is:
    1
    2
    3
    4
    [1, 2, 3] // the provided "even number" version: [0, 2, 4, 9]
    [3, 1, 2] // the provided "even number" version: [4, 9, 0, 2]
    // I thought it should be [3, 2, 1]  dead~
    // So I am totally wrong about it.

By now, I am clear about the intention of the problem.

Ex 4 (HighOrderFunctionsAndArrays)

Problem: link
Code: HigherOrderFunctionsAndArrays.java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public int compare(String s1, String s2) {
  if ((s1 == null) && (s2 == null)) return 0;
  if (s1 == null) return -1;
  if (s2 == null) return 1;
  return s1.length() - s2.length();
}

public static String[][] step(String[][] arr) {
  /* Recall: All String references in stepped are null by
  default, so the edges are correct on initialization */
  String[][] stepped = new String[arr.length][arr[0].length];
  for (int i = 1; i < arr.length - 1; ++i) {
    for (int j = 1; j < arr[0].length - 1; ++j) {
      String[] temp = new String[9];
      // LengthComparator lc = new LengthComparator();
      int count = 0;
      for (int k = -1; k <= 1; k += 1) { /* horizontally */
        for (int m = -1; m <= 1; m += 1) { /* vertically */
          // int index = (k + 1) * 3 + (m + 1);
          // temp[index] = arr[i + k][j + m];
          temp[count] = arr[i + k][j + m];
          count += 1; /** nice! (mapping) */
        }
      }
      // stepped[i][j] = max(temp, lc);
      stepped[i][j] = max(temp, new LengthComparator());
    }
  }
  return stepped;
}

Ex 5 (Squaring a List)

Mutative / Non-mutative + Recursive / Iterative

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/** Non-mutative (new) - Recursive */
public static IntList square_re(IntList L) {
  if (L == null) {
    return null;
  }
  return new IntList(L.first * L.first, square_re(L.rest));
}

/** Non-mutative - Iterative */
public static IntList square(IntList L) {
  if (L == null) {
    return null;
  }
  IntList p = new IntList(L.first * L.first, null);
  IntList ret = p;
  L = L.rest;
  while (L != null) {
    p.rest = new IntList(L.first * L.first, null);
    p = p.rest;
    L = L.rest;
  }
  return ret;
}

/** Mutative - Recursive */
public static IntList squareMutative_re(IntList L) {
  if (L == null) { return null; }
  L.first = L.first * L.first;
  L.rest = squareMutative_re(L.rest);
  return L;
}

/** Mutative - Iterative */
public static IntList squareMutative(IntList L) {
  IntList p = L;
  while (p != null) {
    p.first = p.first * p.first;
    p = p.rest;
  }
  return L;
}

Ex (Discussion 3)

Ex 1 (insert)

Data Structure (Note that no size field):

1
2
3
4
5
6
7
8
public class SLList {
  class IntNode {
    int item;
    IntNode next;
  }

  IntNode first;
}

My Way

Recursive:

Later, I wrote a recursive version. More succinct!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// size == 3
// if pos == 0, first
// if pos == 3, last
// if pos >  3, last
public void insert(int item, int pos) {
  // better check size first; but in this case, no size field
  first = insert(first, item, pos);
}

private IntNode insert(IntNode x, int item, int pos) {
  if (pos <= 0 || x == null) { // consider invalid pos
    return new IntNode(item, x); // return connects to prev
  }
  x.next = insert(x.next, item, pos - 1);
  return x;
}

Iterative:

It is too complicated. Remember the insert pattern I summarize.

This is the code using another count variable. Don’t look at it. Go for the version in the Solution section.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public void insert(int item, int position) {
  if (position == 0 || first == null) {
    addFirst(item); return;
  } /** position >= 1 && first != null */

  IntNode p1 = null;  /* prev node */
  IntNode p2 = first; /* p1 p2 (ahead) */
  int count = 0;
  while (count < position) {
    p1 = p2;
    p2 = p2.next;
    count += 1;
    if (p2 == null) { /* hit the end */
      break;
    }
  }
  p1.next = new IntNode(item, p1.next);
}

Answer

You don’t need extra pointer to remember the previous node. In insert cases, you just need to look ahead, which means currentNode (also the one ptr finally stops at) is the one at pos - 1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 0 1 2 (index)  always use 2~3 nodes to test
// 3 6 2 
/**
 * Case 1: pos == 1, <currentNode> stops at pos 0
 * Case 2: pos == 2, <currentNode> stops at pos 1
 * Case 3: pos >= 3, <currentNode> stops at pos 2 (ending)
 * ----------------------------------------------
 * If pos is valid: <while> stops when pos hits 1
 * If pos is invalid (>3): <while> stops when <currentNode.next> is null
 */
public void insert(int item, int pos) {
  /** 
   * Guarantee [first] is not null, and we are not gonna insert node at (pos 0) since there is no (pos - 1) here. 
   * Unless a <sentinel> is used
   */
  if (first == null || pos == 0) { // consider pos == 0
    addFirst(item);
    return;
  }

  // consider pos == 1
  IntNode currentNode = first; // won't be null
  while (pos > 1 && currentNode.next != null) { // why pos > 1? If pos is 1, currentNode should not move at all.
    pos -= 1;
    currentNode = currentNode.next;
  }
  IntNode newNode = new IntNode(item, currentNode.next);
  currentNode.next = newNode;  // lastNode.next = newNode
}

Count code patterns:

count > 0:

1
2
3
4
5
int count = 3;
while (count > 0) {
  // 3 => 2 => 1 (3 times)
  count -= 1;
}

Equivalent to count >= 1:

1
2
3
4
5
int count = 3;
while (count >= 1) {
  // 3 => 2 => 1 (3 times)
  count -= 1;
}

Ex 1.5 (insert extra)

My solution (answer)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static int[] insert(int[] arr, int item, int position) {
  int[] newArr = new int[arr.length + 1];
  /** copy items before  */
  int i = 0;
  for (i = 0; i < position; i++) {
    newArr[i] = arr[i];
  }
  /** insert */
  newArr[i] = item;
  i++;
  /** copy the items after */
  for (; i < newArr.length; i++) {
    newArr[i] = arr[i - 1];
  }
  return newArr;
}

Ex 2 (reverse)

Iterative version

Use the same data structures above. Reverse elements using the existing IntNode objects (you should not use new).

My Way

Note: Similar to the solution. Just use one extra variable but make it clearer.

My Drawing

p != null:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void reverse() {
  if (first == null || first.next == null) {
    return;
  }
  IntNode prev = null;
  IntNode p = first;

  while (p != null) {
    IntNode temp = p.next;  // record the next
    p.next = prev;  // reverse
    prev = p;  // update prev
    p = temp;  // go to next
  }
  first = prev;
}

p.next != null:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void reverse() {
  if (first == null || first.next == null) { // size = 0 or 1
    return;
  }
  IntNode prev = null;
  IntNode p = first;  // first and first.next are not null
  while (p.next != null) {  // since p should stop at the last node
    IntNode temp = p.next;  // record the next
    p.next = prev;  // reverse
    prev = p;  // update prev
    p = temp;  // go to next
  } /* p finally stops at the last node */
  p.next = prev;
  first = p
}

Answer

The answer just uses the first as my prev, but it turns out to be a bit confusing.

My Drawing

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// first -1-> ptr -2-> ptr.next (temp) -3-> ptr.next.next
public void reverse() {
  if (first == null || first.next == null) {
    return;
  }
  IntNode ptr = first.next;  /* if no ".next", there will be a bug */
  first.next = null; /* -1-> */
  /* How to determine the condition?
   * If ptr is pointing at the last node, we still need to work on it.
   * Although ptr.next is null, we need to change it to the last 2nd node.
   * The nice thing is: first is set at the same time.
   * Next round, ptr is null. So we can go with ptr != null
   */
  while (ptr != null) {
    IntNode temp = ptr.next;
    ptr.next = first; /* -2-> */
    first = ptr; /* changing -3-> needs first */
    ptr = temp;
  }
}

Ex 2.5 (reverse extra - Challenging)

Write a second version that uses recursion.

Combine my way and the answer:

It is a very interesting way of using recursion.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public void reverse() {
  if (first == null) return null;
  first = helper(first); // helper must return the last node!
}

//  node#0   node#1   node#2   ...   last node
//             x      current
//    x      current
private IntList helper(IntList x) {
  if (x == null || x.next == null) { // reach the last node
    return x;
  }
  IntList last = helper(x.next);
  IntList current = x.next;
  current.next = x;
  x.next = null; // originally points to what current now points to
  return last; // last node
}

Same as above (Just do it again when I am reviewing):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// could be skipped (same code)
public void reverse() {
  if (first == null) return null; // size = 0
  first = reverseHelper(first); // helper must return the last node
}

private IntList reverseHelper(IntList x) {
  // ok with size = 1
  if (x == null || x.next == null) { // x finally stops at the last node
    return x; // return the last node to first in the reverse()
  }
  // FOCUS (In the graph)
  IntList newHead = reverseHelper(x.next); // newHead points to the last node
  IntList nextOfX = x.next;
  nextOfX.next = x; // reverse (nextOfX.next.next = x)
  x.next = null; // it would be set correctly in next round
  // or you can write: if (x == first) x.next = null; NOT NECESSARY
  return newHead; // need to return the last node
  }
}

Ex 3 (Array reverse)

1
2
3
4
5
6
7
8
9
10
11
12
13
// consider size = 0, 1, 2, 3
public static void reverse(int[] a) {
  // index:  0  1  2  3  4  5
  // even : [ ][ ][ ][x][ ][ ] size = 6
  // odd  : [ ][ ][x][ ][ ]  size = 5
  int mid = a.length / 2; /* think over it for even and odd cases */
  for (int i = 0; i < mid; i += 1) {
    int j = a.length - i - 1; // mirror element
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
  }
}

Ex 3.5 (Array Reverse Extra)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int[] replicate(int[] arr) {
  int total = 0;
  for (int num : arr) {
    total += num;
  }
  int[] newArr = new int[total];
  int i = 0;
  for (int num : arr) {
    int count = num;
    while (count > 0) { // count loop
      newArr[i] = num;
      i++;
      count--;
    }
  }
  return newArr;
}

Ex (Exam Prep 3)

Ex 1 (Skippify)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void skippify() {
  IntList p = this;
  int skipNum = 1;
  while (p != null) {
    IntList theNext = p.next;
    int count = skipNum;
    while (theNext != null && count > 0) {
      theNext = theNext.next;
      count -= 1;
    }
    p.next = theNext;
    p = theNext;
    skipNum += 1;
  }
}

vs. (similar)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public void skippify() {
  IntList p = this;
  int skipNum = 1;
  while (p != null) {
    IntList next = p.rest;
    for (int = 0; i < skipNum; i += 1) { // skip
      if (next == null) {
        break;
      }
      next = next.rest; // find the next
    } // next stops at yellow node
    p.rest = next; // cut and connect
    p = next;
    skipNum += 1;
  }
}

Ex 2 (Remove Duplicates)

1
2
3
4
5
6
7
8
9
10
11
12
public static void removeDuplicate(IntList p) {
  if (p == null) return;

  while (p.next == null) { // since I need to use p.next in the loop
    // since in the last node, no need to check anymore
    if (p.item == p.next.item) { // found duplicate
      p.next = p.next.next; // no need to update p
    } else { // not duplicate
      p = p.next;
    }
  }
}

Midterm 1 - Notes

KeyGate - Method Selection Problem

Sans - Especially for c, consider the case [1, 2, 3] and y = [2]

Array:

1
2
3
4
5
6
7
8
9
10
11
12
13
// Non-destructively creates a copy of x that contains no y.
public static int[] sans(int[] x, int y) {
  int[] xclean = new int[x.length];
  int count = 0;
  for (int i = 0;i < x.length; i += 1) { // filter
    if (x[i] == y) continue;
    xclean[count] = x[i];
    count += 1;
  }
  int[] ret = new int[count];
  System.arrayCopy(xlcean, 0, ret, 0, count);
  return ret;
}

IntList:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// Same requirement
public static IntList ilsans(IntList x, int y) {
  if (x == null) {
    return null;
  }

  if (x.item == y) { // y
    return ilsans(x.next, y);
  }
  // not y
    return new IntList(x.item, ilsans(x.next, y));
    // IntList ret = new IntList(x.item, x.next);
    // ilsans(x.next, y);
    // return ret;
  }
}

IntList (Destructive):

1
2
3
y = 3
x
1  3  5  7

Bad code (duplicate code):

1
2
3
4
5
6
7
8
9
10
// Destructive
public static IntList dilsans(IntList x, int y) {
  if (x == null) {
    return null;
  }

  if (x.item == y) return dilsans(x.next, y); // y
  dilsans(x.next, y); // not y
  return x;
}

Good code (using x.next = ... to connect)

1
2
3
4
5
6
7
8
9
10
public static IntList dilsans(IntList x, int y) {
  if (x == null) {
    return null;
  }
  x.next = dilsans(x.next, y);
  if (x.item == y) { // y
    return x.next;
  }
  return x; // not y
}

Integer Cache (Lab 3)

Reference: Why is 128==128 false but 127==127 is true when comparing Integer wrappers in Java?

Problem:

1
2
3
4
5
6
7
8
9
Integer a1 = new Integer.valueOf(127);
Integer a2 = new Integer.valueOf(127);
a1 == a2;      // true
a1.equals(a2); // true

Integer a3 = new Integer.valueOf(128);
Integer a4 = new Integer.valueOf(128);
a3 == a4;      // false
a3.equals(a4); // true

Explanation:

1
2
3
4
5
6
7
8
// Java 1.6 source code
public static Integer valueOf(int i) {
  if (i >= -128 && i <= IntegerCache.high) { // IntegerCache.high = 127
    return IntegerCache.cache[i + 128];
  } else {
    return new Integer(i);
  }
}

Therefore, we can manage our integers within the range of $[-128, 127)$ to achieve better performance, or by setting the system property to change the behavior:

1
-Djava.lang.Integer.IntegerCache.high = 999